El Diagrama de Arbol es una grafica que resulta util para organizar los calculos que comptrenden varias etapas. Cada segmento en el Arbol es una etapa del problema. Las ramas de un diagrama de arbol se ponderan por medio de probabilidades.
Es una grafica que resulta util para organizar los calculos que comprenden varias etapas.
Es una representacion grafica que muestra los resultados posibles de una serie de experimentos y respectivas probabilidades.
Un diagrama de arbol es un metodo grafico para identificar todas las partes necesarias para alcanzar algun objetivo final.
PASOS PARA CREAR UN DIAGRAMA DE ARBOL
1. Para construir un diagrama de arbol, empezamos por dibujar un punto grueso del lado izquierdo para representar la raiz del arbol.
2. Abrir a partir del mismo, tantas ramas como elementos tenga el punto A.
3. A partir de cada una de estas, tantas ramas como elementos tenga el conjunto B.
4.Leer el conjunto ordenado resultante sobre cada secuencia de ramas.
EJEMPLO Y SOLUCION
1.Un médico general clasifica a sus pacientes de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de árbol diga en cuantas clasificaciones pueden
estar los pacientes de este médico?
Solución: Si contamos todas las ramas terminales, nos damos cuenta que el número de clasificaciones son 2 x 4 x 3 = 24 mismas que podemos enumerar;
MAN, MAA, MAB, MBN, MBA, MBB, etc.
2. Dos equipos denominados A y B se disputan la final de un partido de baloncesto, aquel equipo que gane dos juegos seguidos o complete un total de tres juegos ganados será el que gane el torneo. Mediante un diagrama de árbol diga de cuantas maneras puede ser ganado este torneo,
EJEMPLO DE DIAGRAMA DE ARBOL IMAGENES

2. EJEMPLO #2

3. EJEMPLO #3
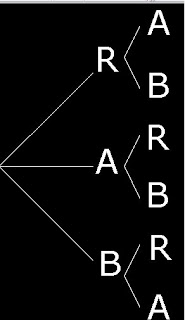
Cuando se quiere calcular la probabilidad de sucesos de experimentos compuestos son muy útiles los diagramas de árbol cuyas ramas nos indican las distintas posibilidades.
EJEMPLO DE DIAGRAMA DE ARBOL IMAGENES

2. EJEMPLO #2

3. EJEMPLO #3

Cuando se quiere calcular la probabilidad de sucesos de experimentos compuestos son muy útiles los diagramas de árbol cuyas ramas nos indican las distintas posibilidades.
VENTAJA : Hay una mejor visualizacion de alternativas de rutas a seguir en un dado proceso
DESVENTAJA :Cuando el proceso es sumamente largo y tedioso. (Mejor utilizar otro método mas eficiente y aparte corto en tiempo)
Solución:
A = gana el equipo A
B = gana el equipo B
En este diagrama se muestran que hay solo diez maneras de que se gane el torneo, que se obtienen contando las ramas terminales de este diagrama de árbol, las que es posible enumerar;
AA, ABB, ABAA, ABABA, ABABB, etc.